Zero-knowledge (ZK) proofs are powering the most recent innovations in web3. They're already being used in products such as Polygon's zkEVM to bring verifiable scalability to Ethereum, and Polygon ID to verify pieces of your identity without revealing any personal information.
In one sentence: ZK proofs allow you to prove something without revealing the thing itself. This has several real-world applications, such as verifying your age without providing your full license/passport information.
But how does this actually work? What's happening behind the scenes to make this possible? In this post, I'll cover everything you need to know about ZK proofs, but leave out the math.
Let's do it!
How Does a ZK Proof Work?
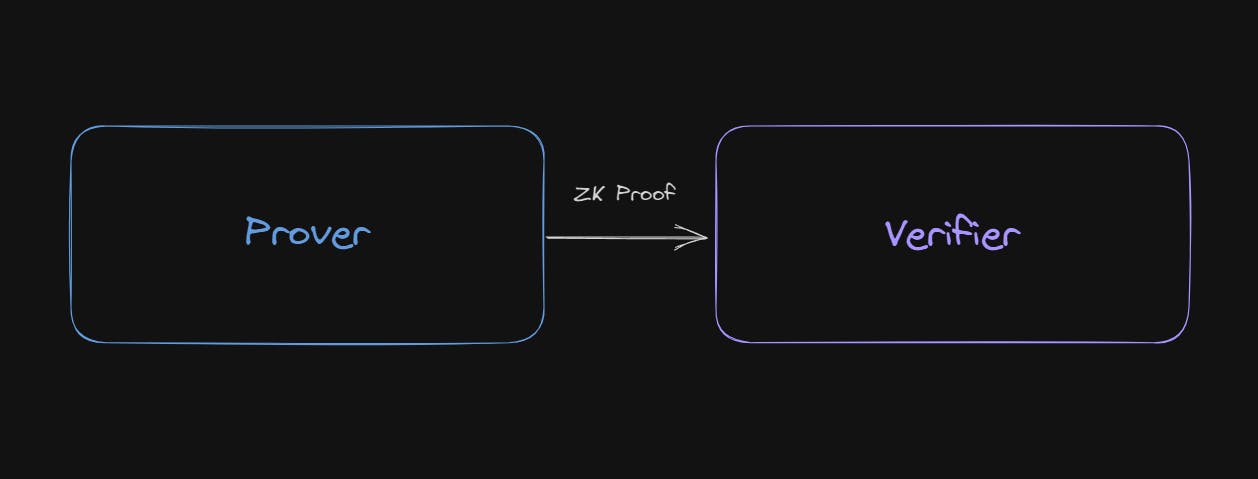
To prove the validity of a statement without revealing the statement itself, there are two parties involved:
The Prover: the person trying to prove something.
The Verifier: the person trying to validate the claim is "real".
Sometimes, there is a third party involved, an issuer, who grants the prover a certificate (such as a license) to the prover, whom the verifier trusts as a source of information.
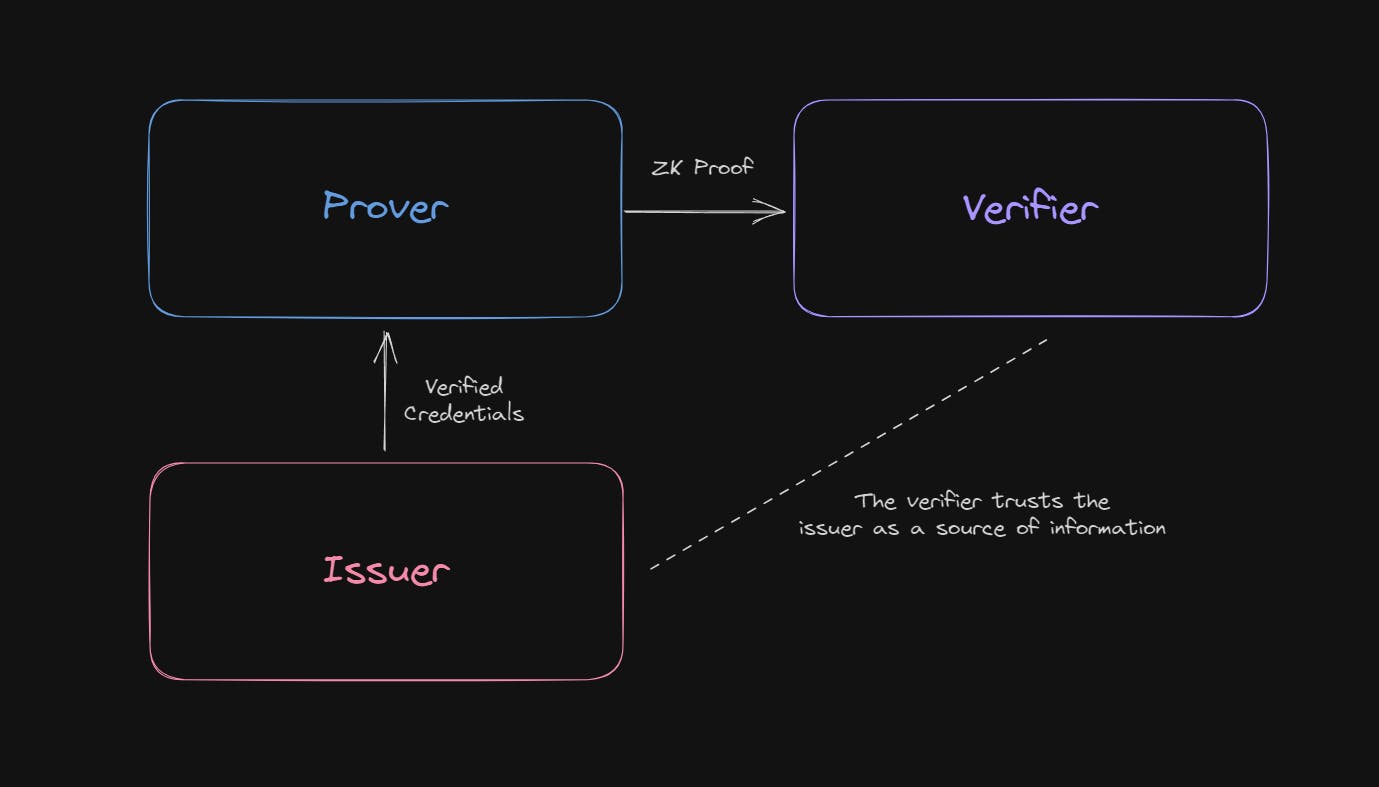
Let's look at an example... I'd like to prove to a website that I am above the age of 18, without uploading a picture of my passport. In this situation, there are:
The Prover: Me, the individual trying to prove I am of legal age.
The Verifier: The website owner, trying to verify that I am of legal age.
The Issuer: The government, that provides me with a passport; a document that the website owner trusts to prove my age.
Typically, I'd need to upload screenshots of my entire passport to the website, (something I really don't want to do), just to prove that I'm over 18.
A fun example made by Steph is applying this to Spongebob. Spongebob wants to prove that his name is in fact Spongebob, but in order to do that, he needs to provide his full license to the verifier (the police officer... or I guess, police fish).
His license contains sensitive information like his DOB, address, gender, and more; all of which isn't necessary to prove his name; but, alas, he has no other choice.

It would be so much better if Spongebob could prove his name, or if I could somehow prove that I'm over 18, without needing to hand over so much sensitive information.
This is a prime example of how ZK proofs provide real value to the world. With ZK proofs, I am now able to prove a part of my identity (or anything else) to a verifier without providing any aspect of my identity, or any supporting documents to prove that fact.
This way, I never transfer sensitive personal information to a third party to be stored in a database; vulnerable to attacks and leaks; something we currently risk almost every time we sign up for a website.
This all sounds great. But how do you prove something without revealing anything about it? For this, we can dive deeper into what ZK proofs are.
What Makes Up A ZK Proof?
So, we want to prove something, without revealing how we know that thing, or what that thing even is. How is that possible?
Before we can answer that, ZK proofs come in two broad categories:
Interactive
Non-interactive
The ones we care about in web3 are non-interactive, but let's quickly touch on what "interactivity" refers to in the context of ZK.
Interactive ZK Proofs
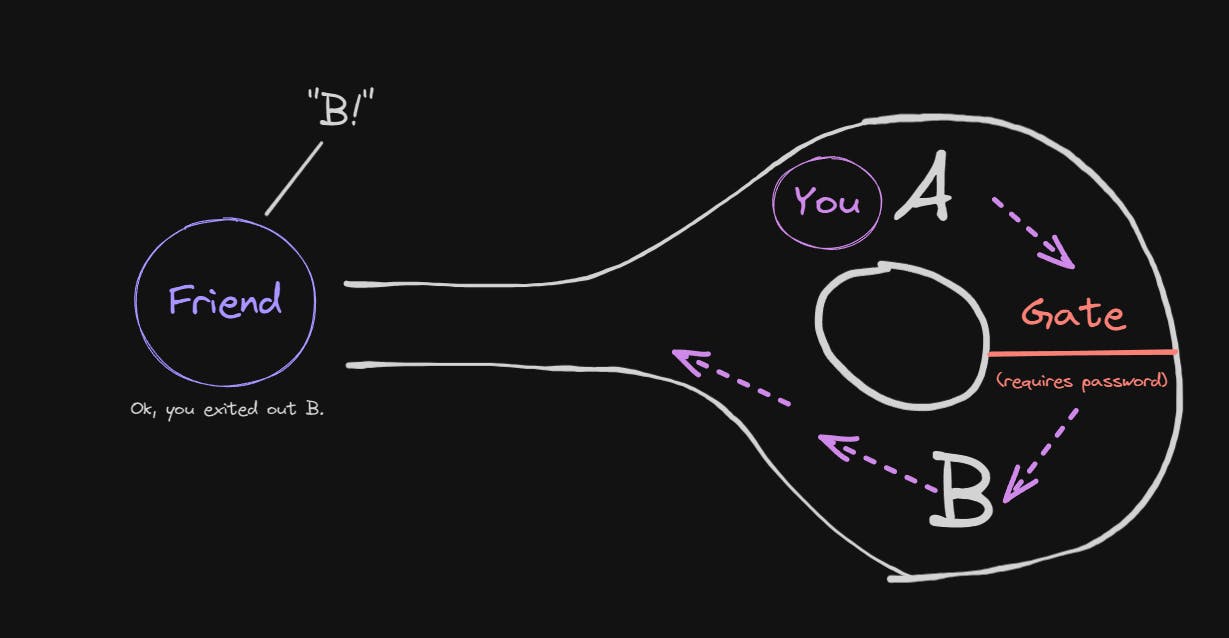
Imagine that there's a ring-shaped cave with a gate inside that requires a secret password to enter through.
Your goal, as the prover is to prove to your friend, the verifier that you know the secret password, called the "witness", without telling them the actual password.

You don't want to tell your friend the password, so instead, you are going to prove you know it; by first, going into one side of the cave randomly; without them seeing.
At this point, your friend doesn't know which side you're on. But as a challenge, they shout out either "A!" or "B!"; requesting you to exit on either side A or side B.
In this simple example, this can lead to two outcomes:
- You entered side A, so you need the password to get through the gate to side B:
- You entered side B, so you don't need the password; you can just walk back out:
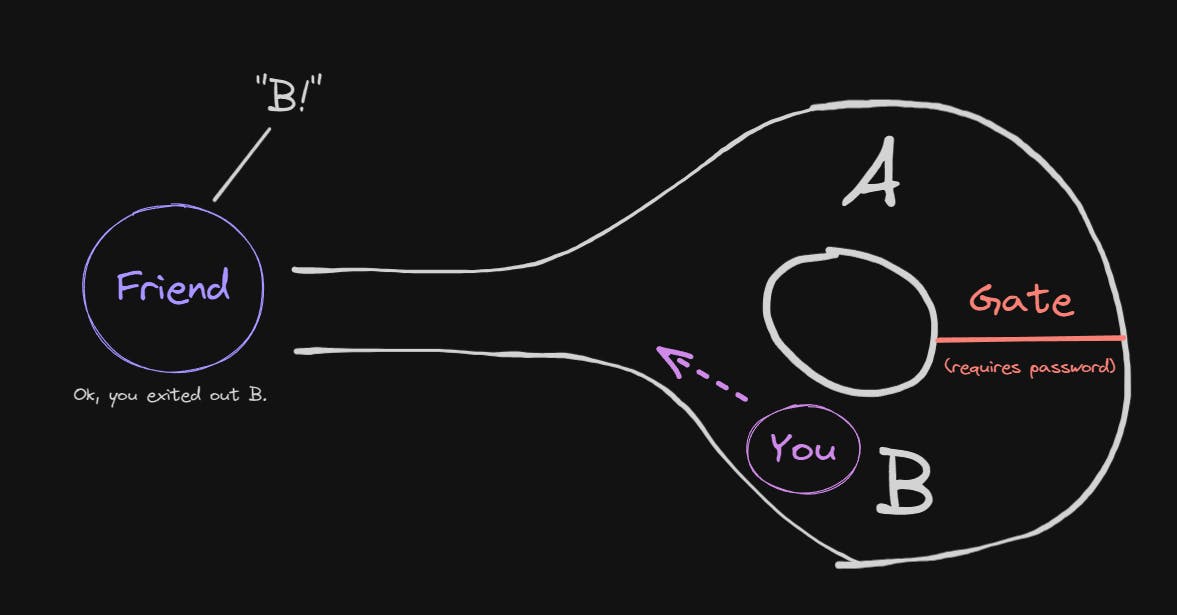
This is called the Ali Baba Cave Story, for reference.
This is a simple example because it's 50/50 whether or not you require the password to satisfy your friend's challenge; thus, doing this challenge only once is not enough to prove with certainty that you know the password.
This means you'd need to complete more iterations of the challenge, correctly exiting either side A or B until your friend is satisfied; or in the theoretical world, until it's impossible for you to have faked knowledge of the witness (the secret code).
Hence, this is interactive; you (the prover) and your friend (the verifier) interact back and forth. Your friend creates a challenge, and you create a response. This cycle repeats until the verifier is satisfied, at which point, the verifier has proven knowledge of the witness.
This makes up the three parts of an interactive ZK proof:
Witness: The secret information the prover wants to prove their knowledge of.
Challenge: The question that only someone with knowledge of the witness would likely be capable of answering; although could be a lucky guess.
Response: The prover's response to the challenge; containing the (hopefully) correct answer.
Steps 2 and 3 are repeated until the verifier is satisfied.
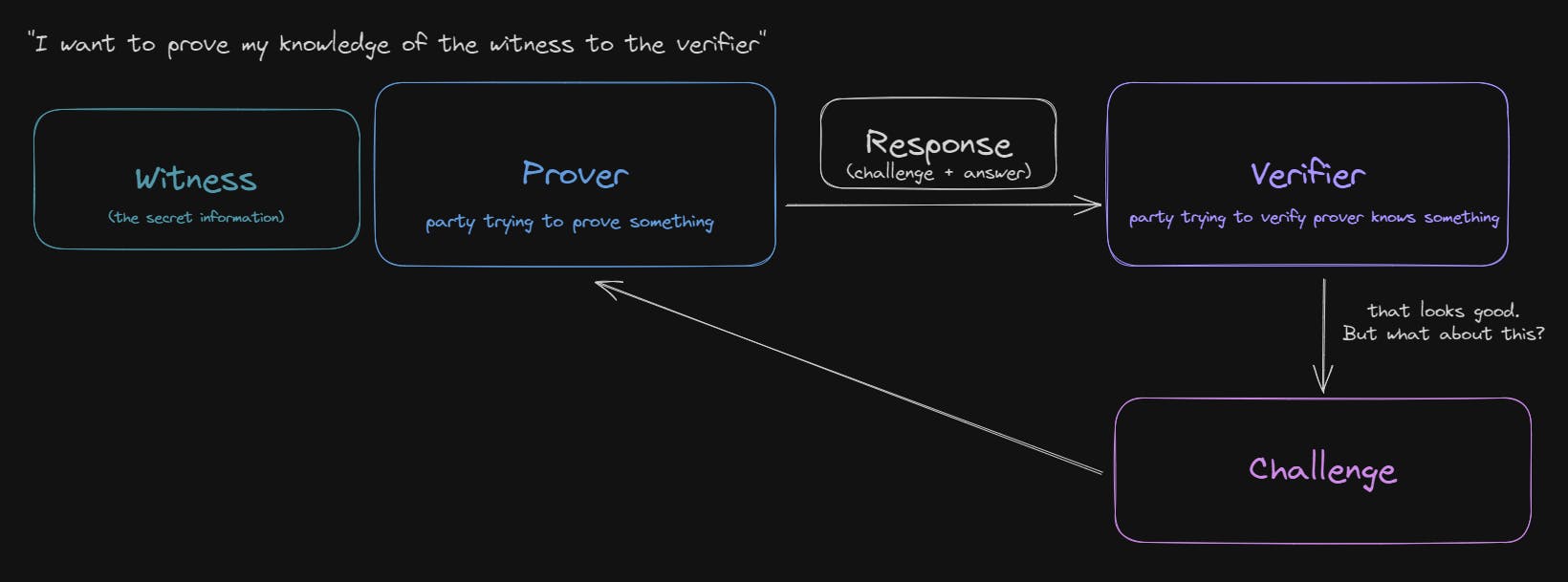
Eventually, once the verifier is satisfied, the cycle breaks; and instead of generating another challenge, the verifier accepts that the prover has knowledge of the witness.
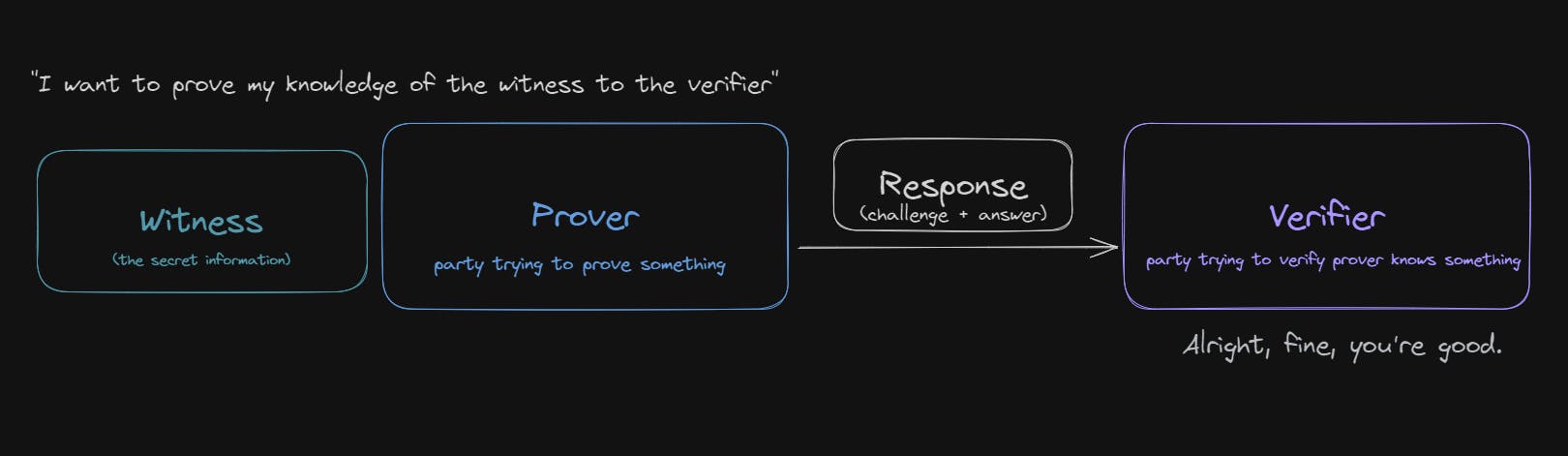
While this process works, it requires many rounds of communication between the prover and verifier; something that is inefficient and doesn't particularly work well in the context of blockchains.
Interactive proofs also have another big limitation; even after the verifier is satisfied, the proof would be unavailable for independent verification; meaning only the party who verified it can trust it, not anyone else.
For these reasons, non-interactive ZK proofs were made.
Non-Interactive ZK Proofs
Non-interactive ZK proofs require only one round of communication from the prover to the verifier. The prover uses an algorithm to compute a ZK proof and sends it to the verifier, who also uses another algorithm to check it.
Another benefit to non-interactive ZK proofs is that they're available for anyone else to verify as well; meaning it's not just proven from the verifier's POV, but available for everyone to verify themselves; suitable for blockchains.
What are these "algorithms" that are capable of proving information and verifying proofs? Well, the answer is; it depends. There are quite a number of them, but two ZKP systems are typically used in the context of blockchain; ZK-SNARKs and ZK-STARKs.
What Are ZK-SNARKs?
ZK-SNARK means Zero-Knowledge Succinct Non-Interactive Argument of Knowledge.
ZK: hopefully by now you can guess what this means (zero-knowledge).
Succinct: they're small, and quickly verifiable by the verifier.
Non-interactive: we discussed this previously. Only one round of communication between the prover and the verifier is required.
Argument: It's theoretically extremely unlikely to be able to "fool" the system.
(Of) Knowledge: It cannot be constructed without access to the secret information (the witness).
They use a cryptographic primitive called elliptic curve pairing as their method of creating and verifying these proofs (we won't go into the math here).
One key thing to note about ZK-SNARKs is that during the initial setup phase, the prover and the verifier must agree to use a "shared key", known as the Common Reference String (CRS). Anyone with access to this shared key can verify the proofs.
This shared key is what makes ZK-SNARKs possible; although this is also arguably their biggest drawback because it creates what is known as a "trusted environment".
The values used to create the CRS, sometimes called "toxic waste" need to be destroyed after the CRS is generated. If they are not, the entire system is at risk; as dishonest provers would be able to compute false proofs; hence, the users must trust that the value is destroyed.
Something also worth mentioning about ZK SNARKs is that they are not "quantum-resistant"; meaning they are vulnerable to attacks by quantum computers in the future; although they could potentially be upgraded in the future to become quantum-resistant.
What Are ZK-STARKs?
ZK-STARK means Zero-Knowledge Scalable Transparent Argument of Knowledge.
Scalable: Rather than being "succinct", they're scalable; meaning they generate and verify proofs with larger witnesses more efficiently than ZK-SNARKs.
Transparent: There's no trusted setup required. They rely on publicly verifiable randomness to generate the shared key.
This improvement in transparency usually comes with a tradeoff of generating much larger proofs than the size of ZK-SNARKs; except when dealing with very large datasets. The size of a proof goes up from 288 bytes to a few hundred kilobytes.
Rather than using elliptic curves, they use polynomials; something I am definitely not qualified to tell you about. Vitalik has a three-part series on this topic: 1, 2, 3.
ZK STARKs address both of the concerns we discussed with ZK-SNARKs, they:
Don't require a "trusted environment".
Are plausibly post-quantum secure; meaning they won't be vulnerable to attacks from quantum computers in the future.
ZK-STARKS are newer than ZK-SNARKs, and Vitalik calls them their "newer, shinier cousin"! 🤠 So, as a quick recap:
| ZK-SNARK | ZK-STARK | |
| Size | Succinct, quickly verifiable | Bigger, but scales more efficiently when proving larger witnesses |
| Security | Requires a trusted environment | Doesn't require a trusted environment |
| Post-Quantum | Not secure, although potentially upgradeable | Secure |
How Does A zkEVM Work?
Now that we've covered how zero-knowledge proofs work and the two common forms of ZKPs that appear in the web3 world, let's explore one of the recent innovations powered by ZKPs; the zkEVM (zero-knowledge Ethereum Virtual Machine).
zkEVMs come in a few different forms; as Vitalik outlines in his blog post "The different types of ZK-EVMs". The one I'll be referencing in this post is the Polygon zkEVM.
The goal of the zkEVM is to improve the scalability of the Ethereum blockchain while remaining secure, decentralized and EVM-compatible.
The details are complicated, but the core principles are the same as what we've discussed so far. As in all ZKP systems, there are:
A Prover: Generates validity proofs representing the truthfulness of a batch of transactions submitted by users.
First, it creates multiple ZK-STARK proofs.
It bundles the ZK-STARKs together using STARK Recursion, to create a single ZK-STARK.
This ZK-STARK is big, so it goes through the CIRCOM component which outputs to the SNARK builder.
As the name suggests, the SNARK builder generates a ZK-SNARK validity proof; this helps in reducing gas costs from 5M to 350K.
A Verifier: The
PolygonZkEVMsmart contract deployed on Ethereum is the verifier of the ZK proofs.
Flow Of Data In A zkEVM
Below, is a simplified flowchart of data in the Polygon zkEVM.
I've broken it up into chronological sections to help it be more digestible.
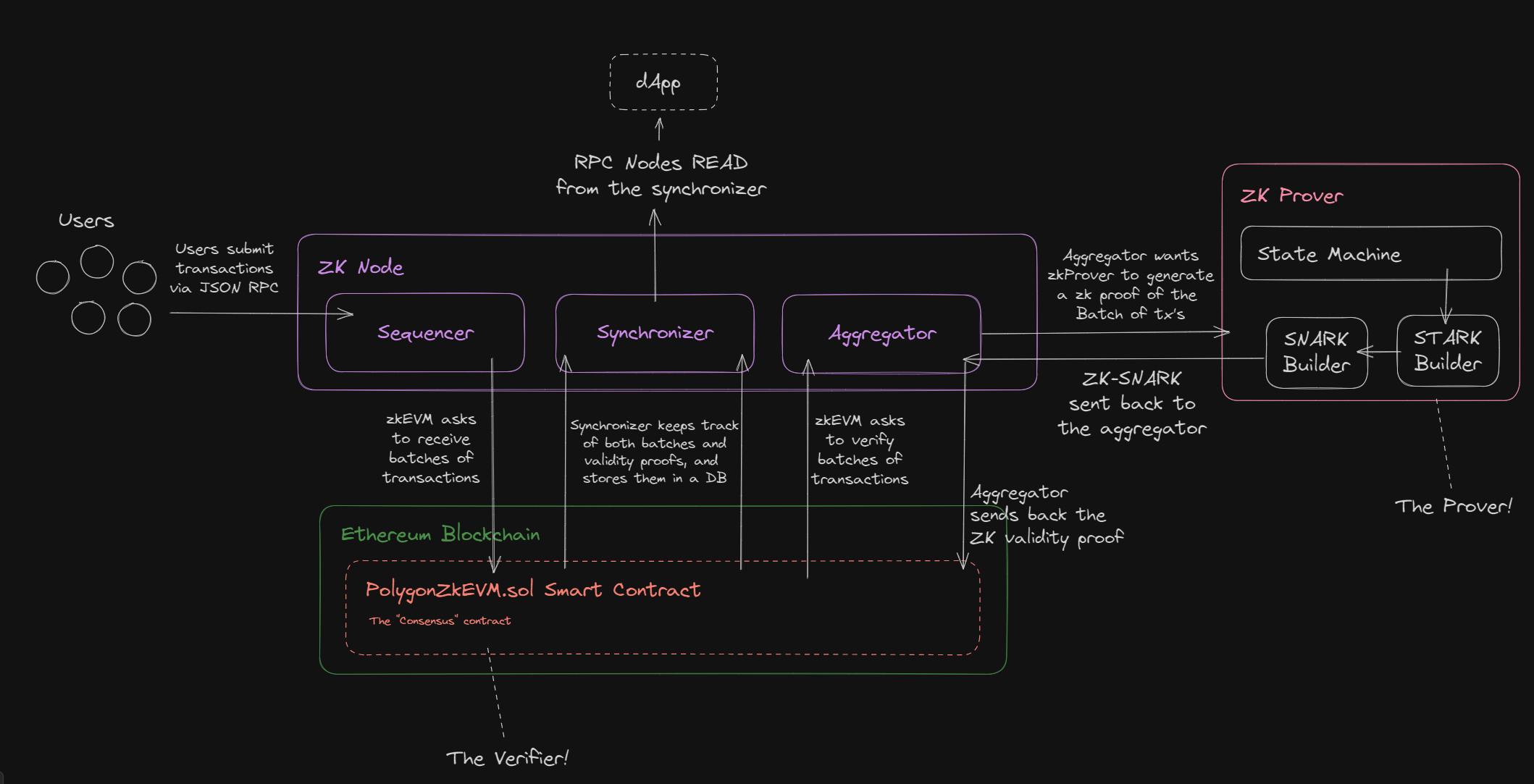
Submitting Transactions
As a user, you submit transactions as you would normally with any other EVM chain such as Ethereum; by signing transactions and sending them through JSON RPC.
A sequencer node running zkEVM software picks these transactions up and decides which ones it wants to process, with some incentive mechanisms in place for doing so correctly.

Batching Transactions
The sequencer batches transactions together into one and submits them to the PolygonZkEvm smart contract, which is stored on Ethereum Mainnet (and a separate instance on Ethereum Goerli testnet).
These batches aren't necessarily correct or verified at this point.
Verifying Transactions
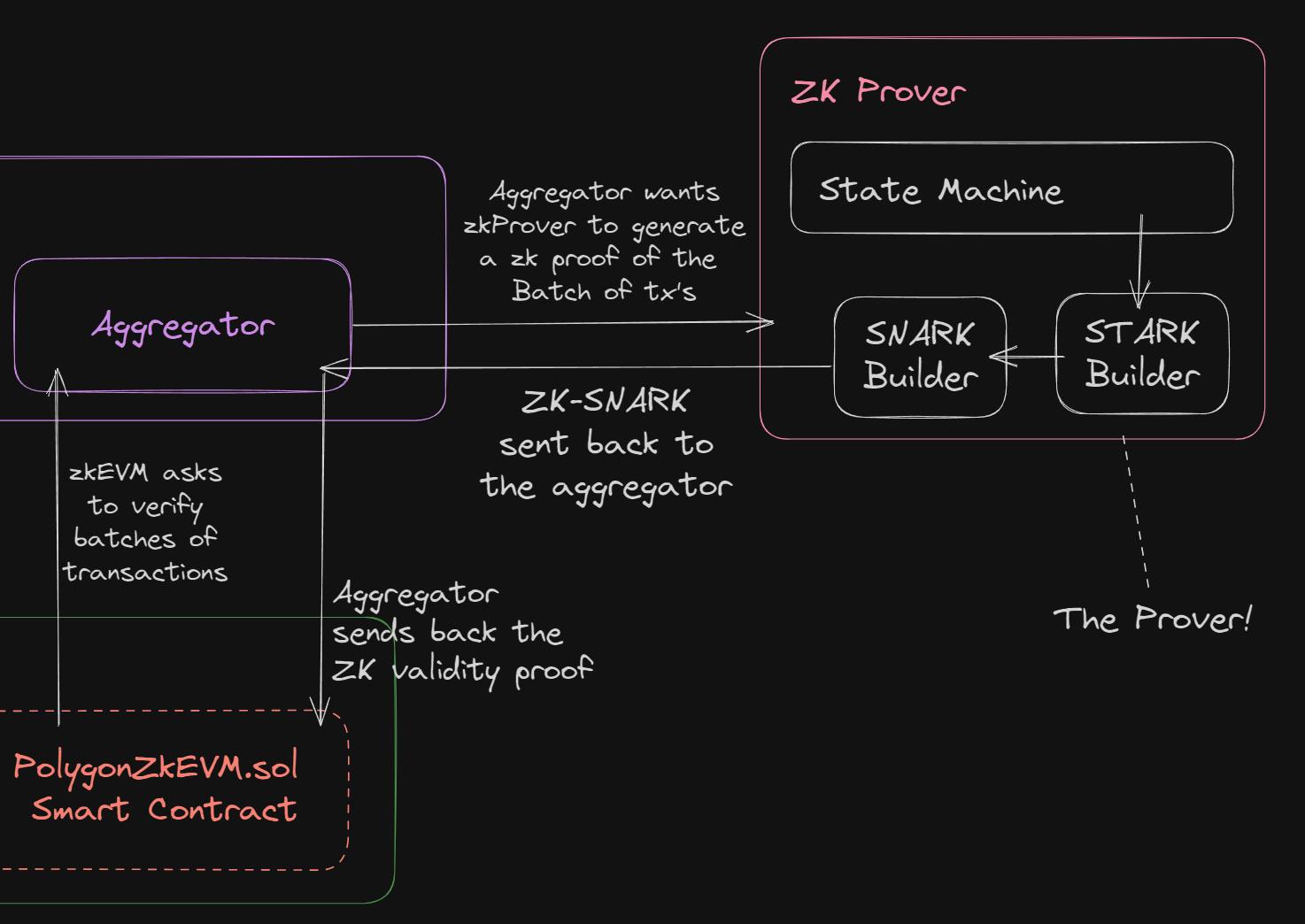
Using ZKPs, the PolygonZkEVM smart contract is acting as the verifier in this setup. It wants to verify that the batch it just received is valid; it does so by sending the batch to an aggregator node.

Generating & Verifying ZK Proofs / Validity Proofs
The PolygonZkEVM smart contract sends the batch it just received to an aggregator node, which is another machine running zkEVM software that communicates with a ZK prover. The flow is as follows:
The aggregator receives the batch from smart contract
The Aggregator sends the batch to ZK Prover
The ZK Prover creates multiple ZK-STARKs -> a single ZK-STARK -> a ZK-SNARK
The ZK-SNARK (the validity proof) gets sent back to the aggregator
The aggregator sends back the validity proof to the
PolygonZkEVMsmart contractThe
PolygonZkEVMSmart contract verifies the validity proofIf the validity proof is valid, accept it.
If it is not valid, reject it.
Reading The ZK EVM
In order for the ZK EVM to be useful, decentralized applications (dApps) need to read information from it; which is where the synchronizer comes into play.
It reads in events from the Ethereum smart contract(s), storing knowledge of both the ZK validity proofs from the aggregator and the batches submitted from the sequencer.
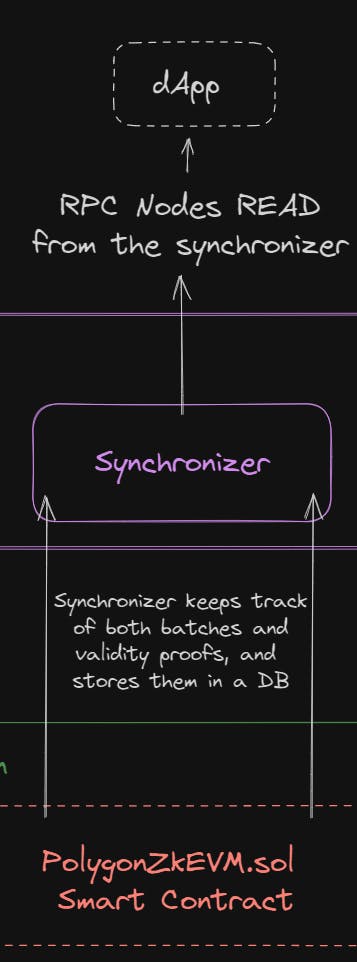
This way, applications can easily get a view of the state of the rollup via JSON RPC.
Wrapping Up
Zero-knowledge proofs are real-world applications of cryptography that could be the foundation of a more privacy-oriented future; demonstrated in products like Polygon ID.
In the context of blockchain, ZKPs are being utilized to improve the scalability of Ethereum in products like Polygon's zkEVM, by providing a new way to verify batches of transactions without the typical loss of security or EVM compatibility we see today with other rollup solutions.
In this post, we've covered:
What ZK Proofs are, and why they're important.
How ZK proofs work, including ZK-SNARKs and ZK-STARKs.
How these proofs are being used in the blockchain world.
If you'd like to learn how you can apply these concepts, I have a previous blog post covering how to build your first smart contract and decentralized application on Polygon zkEVM below:
That's it for this post! Follow me on Twitter to keep up to date with more educational content like this every week: My Twitter.

